Leetcode journey - Question 429. N-ary Tree Level Order Traversal

Problem:

Given an n-ary tree, return the level order traversal of its nodes' values.

Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples).

Example 1:

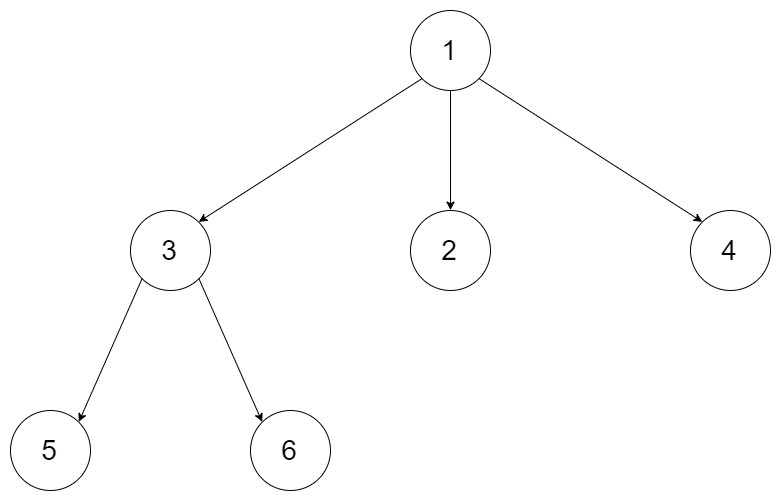
Input: root = [1,null,3,2,4,null,5,6]
Output: [[1],[3,2,4],[5,6]]

Example 2:

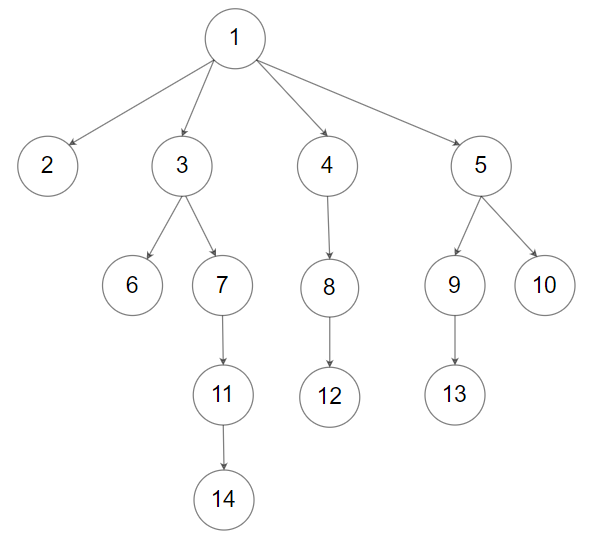
Input: root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
Output: [[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]]

Constraints:

The height of the n-ary tree is less than or equal to 1000
The total number of nodes is between [0, 10⁴]

Solution:

Approach:

We can use a queue to solve this problem.

Then we will push the root node in the queue and then we can pop the node and push all its children in the queue.

Since queue is a FIFO data structure, we can pop the nodes in the order of their level.

We will repeat this process until the queue is empty.

We can use a vector to store the values of the nodes at each level. We will push this vector into the answer vector and then we can clear the vector and repeat the process until the queue is empty.

Pseudo Code:

function levelOrder(root):
    ans = []
    if root is equal to NULL:
        return ans
    make a queue q
    push root in q
    while q is not empty:
        size = size of q
        make a vector temp
        for i = 0 to size:
            curr = front of q
            pop q
            push curr->val in temp
            for j = 0 to size of curr->children:
                push curr->children[j] in q
        push temp in ans
    return ans

Now, we can write the code:

Code:

#include <bits/stdc++.h>
using namespace std;

class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val) {
        val = _val;
    }

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};


class Solution {
public:
    vector<vector<int>> levelOrder(Node* root) {
        vector<vector<int>> ans;
        if(root == NULL){
            return ans;
        }
        queue<Node*> q;
        q.push(root);
        while(!q.empty()){
            int size = q.size();
            vector<int> temp;
            for(int i = 0; i < size; i++){
                Node* curr = q.front();
                q.pop();
                temp.push_back(curr->val);
                for(int j = 0; j < curr->children.size(); j++){
                    q.push(curr->children[j]);
                }
            }
            ans.push_back(temp);
        }
        return ans;

    }
};

Complexity Analysis:

Time Complexity: O(n)
Space Complexity: O(n)
Hope this helps!

If you have any questions, please leave a comment below. 💭
If you like this article, please share it with your friends. 💖
If you want to read more articles like this, please follow me.